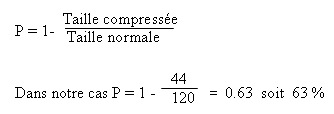Cet algorithme est couramment utilisé pour la compression,
mais son champ d'application ne se restreint pas à ce
domaine. Il est aussi utilisé dans la vidéo et dans
l'audio. En fait, on lui adjoint la plupart du temps une
autre méthode de compression qui, elle, se fait avec perte.
Le principe du codage de Huffman est le suivant : plus un
motif est fréquent, plus il sera codé sur un petit nombre
de bits. Il offre une méthode pour obtenir la manière de
coder les informations à partir de leur probabilité
d'apparition.
1.
Présentation :
La méthode de compression Huffman consiste à diminuer au
maximum le nombre de bits utilisés pour coder un fragment
d’information. Cette méthode est une méthode de compression
sans perte.
Supposons que notre fichier soit extrêmement simple, et
constitué d'une phrase : « Manu fait Huffman ».
Il y a 15 caractères dans ce fichier; chaque caractère
étant codé par un octet de 8bits (codage ASCII). Cela
signifie donc 15 octets, ou encore 120 bits.
Le fragment d’information sera un caractère. Plus le
fragment sera grand, plus les possibilités seront grandes
et donc la mise en œuvre complexe à exécuter. L’algorithme
de Huffman se base sur la fréquence d’apparition d’un
fragment pour le coder : plus un fragment est fréquent,
moins on utilisera de bits pour le coder. Dans notre
exemple de fichier texte, si on considère que notre
fragment est la taille d’un caractère, on peut remarquer
qu’ils n’ont pas tous la même fréquence d’apparition : par
exemple la lettre ‘A’ est largement plus fréquente que la
lettre ‘T’ par conséquent la lettre ‘A’ sera codée sur 2
bits alors que la lettre ‘T’ en prendra 4.
2.
Création de la table des fréquences d’apparition des
fragments :
Cette table consiste en un comptage empirique des fragments
au sein des données à compresser. Reprenons l’exemple d’un
texte : nous allons analyser la phrase : « Manu fait
Huffman »
Pour simplifier l’exemple, nous ignorerons la casse et les
espaces :
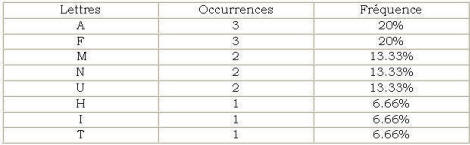
3.
Création de l’arbre.
Nous allons maintenant construire l’arbre à partir de la
liste ordonnée de nœuds. La construction est très facile :
il suffit de prendre les deux nœuds les moins fréquents (I
et T) et de les ajouter comme fils d’un nouveau nœud qui
aura pour fréquence la somme des deux, puis continuer en
ajoutant toujours les plus petits nœuds.
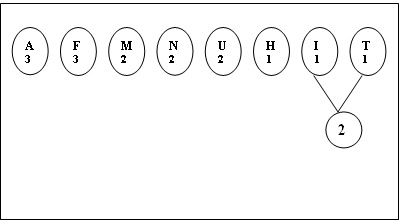
Il suffit de réitérer cette étape jusqu’à ne plus avoir
qu’un seul nœud. Après cela, descendre vers la gauche
équivaut à un 0, et descendre vers la droite à un 1.
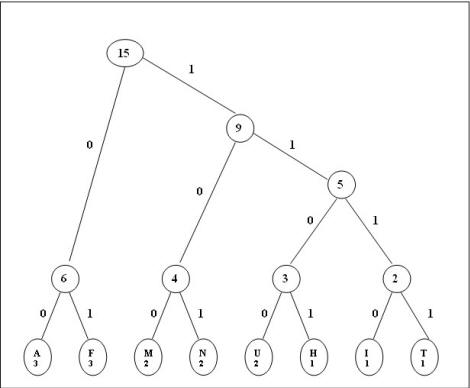
4.
Résultat
Et voici maintenant, transcrit avec notre nouveau code, la
phrase de départ :
10000101110001001110111111011100010110000101
Ce qui nous fait 44 bits, au lieu de 120 au départ! Cela
correspond à un taux de compression de 63 %.
Tableau des lettres codées.
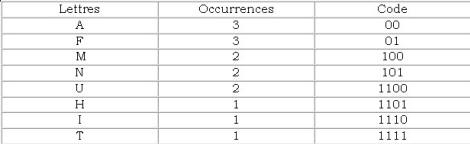
Le fait d'avoir généré un code en se servant d'un arbre
binaire assure qu'aucun code ne peut être le préfixe d'un
autre. Vous pouvez vérifier qu'à l'aide de la table de
codage, il n'y a aucune ambiguïté possible pour décoder
notre mot compressé!
En pratique, la table de codage étant spécifique à chaque
fichier, il est indispensable de l'incorporer au fichier
compressé, de manière à ce que le décryptage soit possible.
Ce qui signifie que la taille du fichier compressé doit
être augmentée d'autant. Dans le cas de notre fichier
exemple, il faudrait incorporer AU MINIMUM 22 octets de
plus pour insérer la table de codage, et le taux de
compression n'est plus aussi bon.
Toutefois, pour des fichiers suffisamment larges (à partir
de quelques kilooctets) le surplus de taille généré par la
table de codage devient négligeable par rapport à
l'ensemble du fichier. Concrètement, l'algorithme de
Huffman permet d'obtenir des taux de compression typiques
compris entre 30% et 60%.
5.
Remarque
On définit le ratio de compression de la manière suivante :