1.
Qu'est-ce que le son?
Le son est une vibration de l'air, c'est-à-dire une suite
de surpressions et de dépressions de l'air par rapport à
une moyenne, qui est la pression atmosphérique. D'ailleurs
pour s'en convaincre, il suffit de placer un objet bruyant
(un réveil par exemple) dans une cloche à vide pour
s'apercevoir que l'objet initialement bruyant n'émet plus
un seul son dès qu'il n'est plus entouré d'air!
La façon la plus simple de reproduire un son actuellement
est de faire vibrer un objet. De cette façon un violon émet
un son lorsque l'archet fait vibrer ses cordes, un piano
émet une note lorsque l'on frappe une touche, car un
marteau vient frapper une corde et la fait vibrer.
Pour reproduire des sons, on utilise généralement des
haut-parleurs. Il s'agit en fait d'une membrane reliée à un
électro-aimant, qui, suivant les sollicitations d'un
courant électrique va aller en avant et en arrière très
rapidement, ce qui provoque une vibration de l'air situé
devant lui, c'est-à-dire du son!
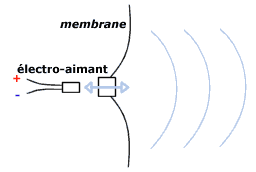
De cette façon on
produit des ondes sonores qui peuvent être représentées sur
un graphique comme les variations de la pression de l'air
(ou bien de l'électricité dans l'électro-aimant) en
fonction du temps. On obtient alors une représentation de
la forme suivante:
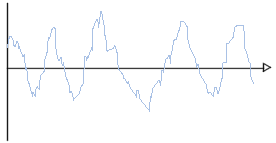
Cette
représentation d'un son est appelée spectre de modulation
d'amplitude (modulation de l'amplitude d'un son en fonction
du temps). Le sonogramme représente par contre la variation
des fréquences sonores en fonction du temps. On peut
remarquer qu'un sonogramme présente une fréquence
fondamentale, à laquelle se superposent des fréquences plus
élevées, appelées harmoniques.
fréquences 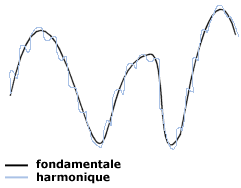
C'est ce qui
permet d'arriver à distinguer plusieurs sources sonores:
les sons graves auront des fréquences basses, et les sons
aigus des fréquences élevées.
2.
L’échantillonnage du son.
Pour pouvoir représenter un son sur un ordinateur, il faut
arriver à le convertir en valeurs numériques, car celui-ci
ne sait travailler que sur ce type de valeurs. Il s'agit
donc de relever des petits échantillons de son (ce qui
revient à relever des différences de pression) à des
intervalles de temps précis. On appelle cette action
l'échantillonnage ou la numérisation du son.
A chaque échantillon (correspondant à un intervalle de
temps) est associé une valeur qui détermine la valeur de la
pression de l'air à ce moment, le son n'est donc plus
représenté comme une courbe continue présentant des
variations mais comme une suite de valeurs pour chaque
intervalle de temps:
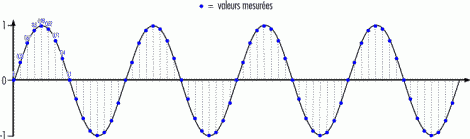
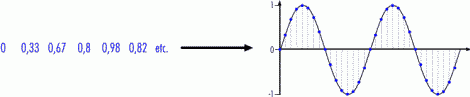
Pour numériser (ou "digitaliser") le
signal, l'ordinateur en mesure la valeur
régulièrement. C'est exactement ce qui se passe quand
l'ordinateur enregistre un fichier son : les valeurs
mesurées sont enregistrées dans le fichier.
0
0,33 0,67 0,8 0,92 0,82 etc.
Pour rejouer le fichier son, l'ordinateur recréé le signal
à partir de chaque valeur enregistrée.
Tous les sons qui nous entourent (musique, bruits...) sont
des vibrations que l'on peut échantillonner de cette
manière.
L'intervalle de temps entre deux échantillons est appelé
taux d'échantillonnage. Etant donné que pour arriver à
restituer un son qui semble continu à l'oreille il faut des
échantillons tous les quelques 100000èmes de seconde, il
est plus pratique de raisonner sur le nombre d'échantillons
par seconde, exprimés en Hertz (Hz).
La valeur du taux d'échantillonnage, pour un CD audio par
exemple, n'est pas arbitraire, elle découle en réalité du
théorème de Shannon. La fréquence d'échantillonnage doit
être suffisamment grande, afin de préserver la forme du
signal. Le Théorème de Nyquist - Shannon stipule que la
fréquence d'échantillonnage doit être égale ou supérieure
au double de la fréquence maximale contenue dans ce signal.
Notre oreille perçoit les sons environ jusqu'à 20000 Hz, il
faut donc une fréquence d'échantillonnage au moins de
l'ordre de 40 000 Hz pour obtenir une qualité
satisfaisante. Il existe un certain nombre de fréquences
d'échantillonnage normalisées :
* 32 kHz : pour la radio FM en numérique (bande passante
limitée à 15 kHz).
* 44.1 kHz : pour l'audio professionnelle et les
compact-disc.
* 48 kHz : pour les enregistreurs numériques multipistes.
professionnels et l'enregistrement grand public (DAT,
Mini-Disc...).
3.
Compression du signal.
Le problème, c'est qu'il faut enregistrer
un très grand nombre de valeurs pour chaque seconde de son.
Cela demande beaucoup de ressource système et occupe
énormément de place sur le disque dur.
Il a donc fallu trouver des moyens pour gagner de la place.
Une des solutions consiste à compresser le signal, c'est à
dire d'utiliser moins de données pour mémoriser la même
information.
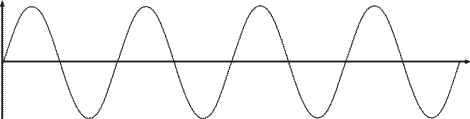
Dans l’exemple suivant, le LA du diapason (celle que vous
avez en frappant un diapason ou en décrochant votre
téléphone), Le signal se répète de la même manière 440 fois
par seconde. On dit qu'il est à 440 Hz.
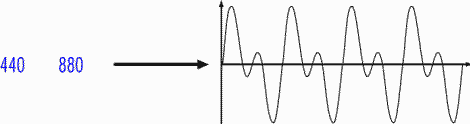
A 880 Hz, la
vibration est deux fois plus rapide et le son plus
aigu: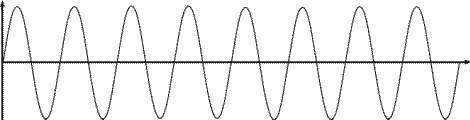
On peut mélanger les deux signaux (440 Hz et 880 Hz):
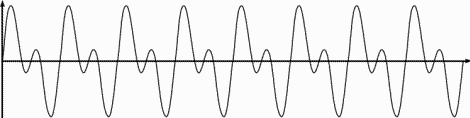
Plutôt que d'enregistrer tous les échantillons (toutes les
valeurs) de ce signal, on pourrait n'enregistrer que les
valeurs 440 et 880. Ainsi, avec seulement 2 valeurs, on
peut reconstituer le signal !
La transformation mathématique qui permet de trouver toutes
les fréquences constituant un signal est appelé transformée
de Fourier.
4. La
transformée de FOURRIER
Définition :
La transformée de Fourier est basée sur la découverte que
toute fonction périodique du temps x(t) peut être
décomposée en une somme infinie de sinus et cosinus dont
les fréquences commencent à zéro et augmentent par
multiples entiers d'une fréquence de base f0 = 1/T, où T
est la période de x(t).
Cette opération mathématique qui consiste à décomposer une
fonction selon ses fréquences. Elle transforme une fonction
f qui dépend du temps, en une nouvelle fonction f’ qui
dépend de la fréquence. Cette nouvelle fonction permet de
décomposer un signal en différentes fréquences.
Représentation.
Reprenons les exemples précédent avec les fréquences 440 Hz
et 880 Hz

Signal de fréquence 440 Hz et d’amplitude A

Signal de fréquence 440 Hz et d’amplitude B

Signal de fréquence 880 Hz et d’amplitude B

Signal de fréquence 440 Hz (d’amplitude A) + signal 880 Hz
(d’amplitude B)
Conclusion.
Une fonction et sa transformée de fourier sont deux aspects
de la même information. La fonction temporelle
correspondant à un enregistrement de musique montre les
variation de la pression de l’air au cours du temps (qui
produisent des ondes sonores), mais elle n’indique pas
quelles fréquences, quelles notes, composent la musique. La
transformé de fourier, en revanche révèle l’information sur
les fréquence et cache l’information sur l’évolution
temporelle : elle donne, pour notre exemple, les fréquences
que la musique comporte, mais il et difficile de savoir
quand ces notes sont jouées.
5.
Représentation du son.
L'ordinateur travaille avec des bits, il faut donc
déterminer le nombre de valeurs que l'échantillon peut
prendre, cela revient à fixer le nombre de bits sur lequel
on code les valeurs des échantillons.
* Avec un codage sur 8 bits, on a 2 puissance 8
possibilités de valeurs, c'est-à-dire 256 valeurs possibles
* Avec un codage sur 16 bits, on a 2 puissance16
possibilités de valeurs, c'est-à-dire 65536 valeurs
possibles
Avec la seconde représentation, on aura bien évidemment une
qualité de son bien meilleure, mais aussi un besoin en
mémoire beaucoup plus important.
Enfin, la stéréophonie nécessite deux canaux sur lesquels
on enregistre individuellement un son qui sera fourni au
haut-parleur de gauche, ainsi qu'un son qui sera diffusé
sur celui de droite.
Un son est donc représenté (informatiquement) par plusieurs
paramètres:
* la fréquence d'échantillonnage.
* le nombre de bits d'un échantillon.
* le nombre de voies (une seule correspond à du mono, deux
à de la stéréo, et quatre à de la quadriphonie).
6.
Mémoire requise pour stocker un son
Il est simple de calculer la taille d'une séquence sonore
non compressée. En effet, en connaissant le nombre de bits
sur lequel est codé un échantillon, on connaît la taille de
celui-ci (la taille d'un échantillon est le nombre de
bits...).
Pour connaître la taille d'une voie, il suffit de connaître
le taux d'échantillonnage, qui va nous permettre de savoir
le nombre d'échantillons par seconde, donc la taille
qu'occupe une seconde de musique. Celle-ci vaut:
Taux d'échantillonnage X Nombre de bits.
Ainsi, pour savoir l'espace mémoire que consomme un extrait
sonore de plusieurs secondes, il suffit de multiplier la
valeur précédente par le nombre de secondes:
Taux d'échantillonnage X Nombre de bits X Nombre de
secondes.
Enfin, la taille finale de l'extrait est à multiplier par
le nombre de voies (elle sera alors deux fois plus
importante en stéréo qu'en mono...).
La taille en bits d'un extrait sonore est ainsi égale à :
Taux d'échantillonnage X Nombre de bits X Nombre de
secondes X Nombre de voies.
